d efficient experimental design

D-efficient or deficient? A robustness analysis of stated choice experimental designs

• Published: 12 December 2017
• Volume 84 , pages 215–238, ( 2018 )

Cite this article

• Joan L. Walker   ORCID: orcid.org/0000-0002-4407-0823 1 ,
• Yanqiao Wang 2 ,
• Mikkel Thorhauge 3 &
• Moshe Ben-Akiva 4  

4579 Accesses

84 Citations

Explore all metrics

This paper is motivated by the increasing popularity of efficient designs for stated choice experiments. The objective in efficient designs is to create a stated choice experiment that minimizes the standard errors of the estimated parameters. In order to do so, such designs require specifying prior values for the parameters to be estimated. While there is significant literature demonstrating the efficiency improvements (and cost savings) of employing efficient designs, the bulk of the literature tests conditions where the priors used to generate the efficient design are assumed to be accurate. However, there is substantially less literature that compares how different design types perform under varying degree of error of the prior. The literature that does exist assumes small fractions are used (e.g., under 20 unique choice tasks generated), which is in contrast to computer-aided surveys that readily allow for large fractions. Further, the results in the literature are abstract in that there is no reference point (i.e., meaningful units) to provide clear insight on the magnitude of any issue. Our objective is to analyze the robustness of different designs within a typical stated choice experiment context of a trade-off between price and quality. We use as an example transportation mode choice, where the key parameter to estimate is the value of time (VOT). Within this context, we test many designs to examine how robust efficient designs are against a misspecification of the prior parameters. The simple mode choice setting allows for insightful visualizations of the designs themselves and also an interpretable reference point (VOT) for the range in which each design is robust. Not surprisingly, the D-efficient design is most efficient in the region where the true population VOT is near the prior used to generate the design: the prior is $20/h and the efficient range is $10–$30/h. However, the D-efficient design quickly becomes the most inefficient outside of this range (under $5/h and above $40/h), and the estimation significantly degrades above $50/h. The orthogonal and random designs are robust for a much larger range of VOT. The robustness of Bayesian efficient designs varies depending on the variance that the prior assumes. Implementing two-stage designs that first use a small sample to estimate priors are also not robust relative to uninformative designs. Arguably, the random design (which is the easiest to generate) performs as well as any design, and it (as well as any design) will perform even better if data cleaning is done to remove choice tasks where one alternative dominates the other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Understanding valuation of travel time changes: are preferences different under different stated choice design settings.

Construction of symmetric paired choice experiments: minimising runs and maximising efficiency

Frontiers in Modeling Discrete Choice Experiments: A Benefit Transfer Perspective

Adamowicz, W., Louviere, J., & Williams, M. (1994). Combining revealed and stated preference methods for valuing environmental amenities . San diego: Academic Press Inc JNL-Comp Subscriptions.

Google Scholar  

Belenky, P. (2011). Revised departmental guidance on valuation of travel time in economic analysis (Revision 2) . Washington DC: Department of Transportation.

Bliemer, M. C. J., & Collins, A. T. (2016). On determining priors for the generation of efficient stated choice experimental designs. The Journal of Choice Modelling , 21 , 10–14.

Article   Google Scholar  

Bliemer, M. C. J., & Rose, J. M. (2010a). Serial choice conjoint analysis for estimating discrete choice models. In S. Hess & A. Daly (Eds.), Choice modelling: The State-of-the-art and the State-of-practice (Proceedings from the inaugural International Choice Modelling Conference) (pp. 139–161). Bingley: Emerald Group Publishing.

Bliemer, M. C. J., & Rose, J. M. (2010b). Construction of experimental designs for mixed logit models allowing for correlation across choice observations. Transportation Research Part B: Methodological , 6 , 720–734.

Bliemer, M. C. J., & Rose, J. M. (2011). Experimental design influences on stated choice outputs: An empirical study in air travel choice. Transportation Research Part A: Policy and Practice , 1 , 63–79.

Bliemer, M. C. J., Rose, J. M., & Chorus, C. G. (2017). Detecting dominance in stated choice data and accounting for dominance-based scale differences in logit models. Transportation Research Part B: Methodological , 201 , 83–104.

Bliemer, M. C. J., Rose, J. M., & Hensher, D. A. (2009). Efficient stated choice experiments for estimating nested logit models. Transportation Research Part B: Methodological , 1 , 19–35.

Bliemer, M. C. J., Rose, J. M., & Hess, S. (2008). Approximation of Bayesian efficiency in experimental choice designs. Journal of Choice Modelling , 1 , 98–126.

Bradley, M., & Bowy, P. H. L. (1984). A stated preference analysis of bicyclist route choice (pp. 39–53). Summer Annual Meeting, Sussex: PTRC.

Burgess, L., & Street, D. J. (2005). Optimal designs for choice experiments with asymmetric attributes. Journal of Statistical Planning and Inference , 1 , 288–301.

ChoiceMetrics, (2012a). Ngene 1.0.2 User Manual & Reference Guide, version: 4/02/2010, ChoiceMetrics Pty Ltd.

ChoiceMetrics, (2012b) Ngene software, version: 1.1.1, Build: 305, developed by Rose, John M.; Collins, Andrew T.; Bliemer, Michiel C.J.; Hensher, David A., ChoiceMetrics Pty Ltd

Cummings, R. G., Brookshire, D. S., & Schulze, W. D. (Eds.). (1986). Valuing environmental goods: A state of the arts assessment of the contingent method . Totowa: Rowman and Allanheld.

Davidson, J. D. (1973). Forecasting Traffic on STOL. Operational Research Quarterly , 4 , 561–569.

Fosgerau, M., & Börjesson, M. (2015). Manipulating a stated choice experiment. Journal of Choice Modelling , 16 , 43–49.

Fowkes, A. S. (2000). Recent developments in state preference techniques in transport research. In J. D. D. Ortuzar (Ed.), Stated preference modelling techniques (pp. 37–52). London: PTRC Education and Research Services.

Hensher, D. A., & Louviere, J. J. (1983). Identifying individual preferences for international air fares-an application of functional-measurement theory . Bath: Univ Bath.

Hensher, D. A. (1982). Functional-measurement, individual preference and discrete-choice modeling-theory and application. Journal of Economic Psychology , 4 , 323–335.

Hensher, D. A. (1994). Stated preference analysis of travel choices-the state of practice . Dordrecht: Kluwer Academic Publ.

Johnson, F. R., Kanninen, B., Bingham, M., & Özdemir, S. (2007). Experimental design for stated choice studies. In B. J. Kanninen (Ed.), Valuing environmental amenities using stated choice studies (pp. 159–202). Dordrecht: Springer.

Chapter   Google Scholar  

Johnson, F. R., Lancsar, E., Marshall, D., Kilambi, V., Muehlbacher, A., Regier, D. A., et al. (2013). Constructing experimental designs for discrete-choice experiments: Report of the ISPOR conjoint analysis experimental design good research practices task force. Value in Health , 1 , 3–13.

Kanninen, B. J. (2002). Optimal design for multinomial choice experiments. Journal of Marketing Research , 2 , 214–227.

Kocur, G., Adler, T., Hyman, W., & Audet, E. (1982). Guide to forecasting travel demand with direct utility measurement . USA Department of Transportation, UMTA: Washington D. C.

Kuhfeld, W. F., Tobias, R. D., & Garratt, M. (1994). Efficient Experimental Design with Marketing Research Applications. Journal of Marketing Research (JMR) , 31 (4), 545–557.

Louviere, J. J., & Hensher, D. (1982). Design and analysis of simulated choice or allocation experiments in travel choice modeling. Transportation Research Record , 890 , 11–17.

Louviere, J. J., & Hensher, D. A. (1983). Using discrete choice models with experimental-design data to forecast consumer demand for a unique cultural event. Journal of Consumer Research , 3 , 348–361.

Louviere, J. J., & Kocur, G. (1983). The magnitude of individual-level variations in demand coefficients: A Xenia Ohio case example. Transportation Research, Part A , 5 , 363–373.

Louviere, J. J., & Woodworth, G. (1983). Design and analysis of simulated consumer choice or allocation experiments - an approach based on aggregate data. Journal of Marketing Research , 4 , 350–367.

Louviere, J. J., Meyer, R., Stetzer, F., & Beavers, L. L. (1973). Theory, methodology and findings in mode choice behavior Working Paper No., The Institute of Urban and Regional Research . Iowa City: The University of Iowa.

Mitchell, R. C., & Carson, R. T. (Eds.). (1989). Using Surveys to Value Public-Goods - The Contingent Valuation Method. Press for Resources for the Future . Baltimore: John Hopkins Univ.

Ojeda-Cabral, M., Hess, S. & Batley, R. (2016). Understanding valuation of travel time changes: are preferences different under different stated choice design settings? Transportation, 1-21.

Rose, J. M., & Bliemer, M. C. J. (2008). Stated preference experimental design strategies. In D. A. Hensher & K. Button (Eds.), Handbook in transport (2nd ed.). Oxford: Elsevier Science.

Rose, J. M., & Bliemer, M. C. J. (2009). Constructing efficient stated choice experimental designs. Transport Reviews , 5 , 587–617.

Rose, J. M., & Bliemer, M. C. J. (2013). Sample size requirements for stated choice experiments. Transportation , 40 (5), 1021–1041.

Rose, J. M., & Bliemer, M. C. J. (2014). Stated choice experimental design theory: The who, the what and the why ch. 7. In S. Hess & A. Daly (Eds.), Handbook of Choice Modelling (pp. 152–177). Cheltenham: Edward Elgar Publishing.

Rose, J. M., Bliemer, M. C. J., Hensher, D. A., & Collins, A. T. (2008). Designing efficient stated choice experiments in the presence of reference alternatives. Transportation Research Part B , 4 , 395–406.

Sándor, Z., & Wedel, M. (2001). Designing Conjoint Choice Experiments Using Managers’ Prior Beliefs. Journal of Marketing Research , 38 (4), 430–444.

Sándor, Z., & Wedel, M. (2002). Profile construction in experimental choice designs for mixed logit models. Marketing Science , 21 (4), 455–475.

Small, K. A. (1982). The scheduling of consumer activities: Work trips. American Economic Review , 3 , 467–479.

Street, D. J., & Burgess, L. (2004). Optimal and near-optimal pairs for the estimation of effects in 2-level choice experiments. Journal of Statistical Planning and Inference , 1–2 , 185–199.

Street, D. J., Bunch, D. S., & Moore, B. J. (2001). Optimal designs for 2k paired comparison experiments. Communications in Statistics - Theory and Methods , 10 , 2149–2171.

Street, D. J., Burgess, L., & Louviere, J. J. (2005). Quick and easy choice sets: Constructing optimal and nearly optimal stated choice experiments. International Journal of Research in Marketing , 4 , 459–470.

Thorhauge, M., Cherchi, E. & Rich, J. (2014). Building efficient stated choice design for departure time choices using the scheduling model: Theoretical considerations and practical implications, Selected Proceedings from the Annual Transport Conference, Aalborg University, Denmark.

Thorhauge, M., Cherchi, E., & Rich, J. (2016a). How flexible is flexible? Accounting for the effect of rescheduling possibilities in choice of departure time for work trips. Transportation Research Part A: Practice and Policy , 86 , 177–193.

Thorhauge, M., Haustein, S., & Cherchi, E. (2016b). Social psychology meets microeconometrics: Accounting for the theory of planned behaviour in departure time choice. Transportation Research Part F: Traffic Psychology and Behaviour , 38 , 94–105.

Toner, J.P., Clark, S.D., Grant-Muller, S. & Fowkes, A.S. (1999). Anything you can do, we can do better: A provocative introduction to a new approach to stated preference design, World Transport Research, Vol 1-4.

Walker, J. L., Wang, Y., Mikkel, T., & Ben-Akiva, E. (2015). D-EFFICIENT OR DEFICIENT? A robustness analysis of stated choice experimental designs, presented at the 94th annual meeting of the Transportation Research Board . Washington: D. C.

Download references

Acknowledgements

An earlier draft of this work was initially presented at the Transportation Research Board annual meeting in January of 2015 (Walker et al. 2015 ), and we thank the reviewers from that process as well as the discussion that followed from the presentation and circulation of the working paper. We thank Andre de Palma and Nathalie Picard for organizing the symposium in honor of Daniel McFadden and for following it up with this special issue. We thank two anonymous reviewers assigned by this journal. We also thank Michael Galczynski for the idea for the title.

Author information

Authors and affiliations.

Department of Civil and Environmental Engineering, Center for Global Metropolitan Studies, University of California, Berkeley, 111 McLaughlin Hall, Berkeley, CA, 94720, USA

Joan L. Walker

Department of Civil and Environmental Engineering, University of California, Berkeley, 116 McLaughlin Hall, Berkeley, CA, 94720, USA

Yanqiao Wang

Department of Management Engineering, Technical University of Denmark, Bygningstorvet 116B, 2800, Kongens Lyngby, Denmark

Mikkel Thorhauge

Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Room 1-181, 77 Massachusetts Avenue, Cambridge, MA, 02139, USA

Moshe Ben-Akiva

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Joan L. Walker .

Rights and permissions

Reprints and permissions

About this article

Walker, J.L., Wang, Y., Thorhauge, M. et al. D-efficient or deficient? A robustness analysis of stated choice experimental designs. Theory Decis 84 , 215–238 (2018). https://doi.org/10.1007/s11238-017-9647-3

Download citation

Published : 12 December 2017

Issue Date : March 2018

DOI : https://doi.org/10.1007/s11238-017-9647-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Stated choice experiments
• Mode choice model
• Value-of-time
• Experimental design
• D-efficient
• Find a journal
• Publish with us
• Track your research

• standard factorial or fractional factorial designs require too many runs for the amount of resources or time allowed for the experiment
• the design space is constrained (the process space contains factor settings that are not feasible or are impossible to run).

• DSpace@MIT Home
• MIT Open Access Articles

D-efficient or deficient? A robustness analysis of stated choice experimental designs

Open Access Policy

Creative Commons Attribution-Noncommercial-Share Alike

Terms of use

Date issued, collections.

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

EDT: Efficient designs for Discrete Choice Experiments

Folders and files

Repository files navigation.

EDT is a Python-based tool to construct D-efficient designs for Discrete Choice Experiments. EDT combines enough flexibility to construct from simple 2-alternative designs with few attributes, to more complex settings that may involve conditions between attributes.

While EDT designs are based on the widely-used D-efficiency criterion (see Kuhfeld, 2005), it differs from other free- or open-source efficient design tools (such as idefix for R) on the use of a Random Swapping Algorithm based on the work of Quan, Rose, Collins and Bliemer (2011), obtaining significant speed improvements to reach an optimal design, to a level that competes with well-known paid software such as NGene.

The main features of EDT are:

Allows to customize each attribute in terms of:

• Attribute Levels
• Continuous or Dummy coding (Effects coding is work-in-progress)
• Assignement of prior parameters
• Attribute names

Designs with constraints: EDT allows to define conditions over different attribute levels.

Designs with blocks.

Designs with alternative-specific constants (ASC).

Multiple stopping criteria (Fixed number of iterations, iterations without improvement or fixed time).

Allows to export the output design in an Excel file.

Any contributions to EDT are welcome via this Git, or to the email joseignaciohernandezh at gmail dot com.

• Kuhfeld, W. F. (2005). Experimental design, efficiency, coding, and choice designs. Marketing research methods in SAS: Experimental design, choice, conjoint, and graphical techniques , 47-97.
• Quan, W., Rose, J. M., Collins, A. T., & Bliemer, M. C. (2011). A comparison of algorithms for generating efficient choice experiments.

Contributors 2

• Python 100.0%

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 31 July 2018

POINTS OF SIGNIFICANCE

Optimal experimental design

• Byran Smucker 1 ,
• Martin Krzywinski 2 &
• Naomi Altman 3  

Nature Methods volume  15 ,  pages 559–560 ( 2018 ) Cite this article

28k Accesses

69 Citations

20 Altmetric

Metrics details

Customize the experiment for the setting instead of adjusting the setting to fit a classical design.

You have full access to this article via your institution.

To maximize the chance for success in an experiment, good experimental design is needed. However, the presence of unique constraints may prevent mapping the experimental scenario onto a classical design. In these cases, we can use optimal design: a powerful, general-purpose tool that offers an attractive alternative to classical design and provides a framework within which to obtain high-quality, statistically grounded designs under nonstandard conditions. It can flexibly accommodate constraints, is connected to statistical quantities of interest and often mimics intuitive classical designs.

For example, suppose we wish to test the effects of a drug’s concentration in the range 0–100 ng/ml on the growth of cells. The cells will be grown with the drug in test tubes, arranged on a rack with four shelves. Our goal may be to determine whether the drug has an effect and precisely estimate the effect size or to identify the concentration at which the response is optimal. We will address both by finding designs that are optimal for regression parameter estimation as well as designs optimal for prediction precision.

To illustrate how constraints may influence our design, suppose that the shelves receive different amounts of light, which might lead to systematic variation between shelves. The shelf would therefore be a natural block 1 . Since we don’t expect such systematic variation within a shelf, the order of tubes on a shelf can be randomized. Furthermore, each shelf can only hold nine test tubes. The experimental design question, then, is: What should be the drug concentration in each of the 36 tubes?

If concentration were a categorical factor, we could compare the mean response at nine concentrations—a traditional randomized complete block design (RCBD) 1 . However, because concentration is actually continuous, discrete levels unduly limit which concentrations are studied and reduce our ability to detect an effect and estimate the concentration that produces an optimal response. Classical designs, like full factorials or RCBDs, assume an ideal and simple experimental setup, which may be inappropriate for all experimental goals or untenable in the presence of constraints.

Optimal design provides a principled approach to accommodating the entire range of concentrations and making full use of each shelf’s capacity. It can incorporate a variety of constraints such as sample size restrictions (e.g., the lab has a limited supply of test tubes), awkward blocking structures (e.g., shelves have different capacities) or disallowed treatment combinations (e.g., certain combinations of factor levels may be infeasible or otherwise undesirable).

To assist in describing optimal design, let’s review some terminology. The drug is a ‘factor’, and particular concentrations are ‘levels’. A particular combination of factor levels is a ‘treatment’ (with just a single factor, a treatment is simply a factor level) applied to an ‘experimental unit’, which is a test tube. The shelves are ‘blocks’, which are collections of experimental units that are similar in traits (e.g., light level) that might affect the experimental outcome 1 . The possible set of treatments that could be chosen is the ‘design space’. A ‘run’ is the execution of a single experimental unit, and the ‘sample size’ is the number of runs in the experiment.

Optimal design optimizes a numerical criterion, which typically relates to the variance or other statistically relevant properties of the design, and uses as input the number of runs, the factors and their possible levels, block structure (if any), and a hypothesized form of the relationship between the response and the factors. Two of the most common criteria are the D-criterion and the I-criterion. They are fundamentally different: the D-criterion relates to the variance of factor effects, and the I-criterion addresses the precision of predictions.

To understand the D-criterion (determinant), suppose we have a quadratic regression model 2 with parameters β 1 and β 2 that relate the factor to the response (for simplicity, ignore β 0 , the intercept). Our estimates of these parameters, \(\hat \beta _1\) and \(\hat \beta _2\) , will have error and, assuming the model error variance is known, the D-optimal design minimizes the area of the ellipse that defines the joint confidence interval for the parameters (Fig. 1 ). This area will include the true values of both β 1 and β 2 in 95% (or some other desired proportion) of repeated executions of the design, and its size and shape are a function of the data’s overall variance and the design.

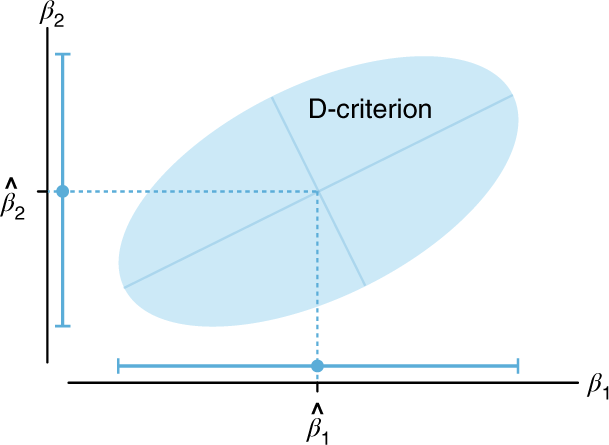
The ellipse can be projected onto each axis to obtain the familiar one-dimensional confidence intervals for each parameter (shown as blue points with error bars). The D-criterion reduces the variance of the parameter estimates and/or the correlation between the estimates by minimizing the area of the ellipse.

On the other hand, the I-criterion (integrated variance) is used when the experimental goal is to make precise predictions of the response, rather than to obtain precise estimates of the model parameters. An I-optimal design chooses the set of runs to minimize the average variance in prediction across the joint range of the factors. The prediction variance is a function of several elements: the data’s overall error variance, the factor levels at which we are predicting, and also the design itself. This criterion is more complicated mathematically because it involves integration.

For both criteria, numerical heuristics are used in the optimization but they do not guarantee a global optimum. For most scenarios, however, near-optimal designs are adequate and not hard to obtain.

Returning to our example, suppose we wish to obtain a precise estimate of our drug’s effect on the mean response. If we expect that the effect is linear (our model has one parameter of interest, β 1 , which is the slope), the D-optimal design places either four or five experimental units in each block at the low level (0 ng/ml) and the remaining units at the high level (100 ng/ml). Thus, to obtain a precise estimate of β 1 , we want to place the concentration values as far apart as possible in order to stabilize the estimate. Assigning four or five units of each concentration to each shelf helps to reduce the confounding of drug and shelf effects.

One downside to this simple low–high design is its inability to detect departures from linearity. If we expect that, after accounting for block differences, the relationship between the response and the factor may be curvilinear (with both a linear and quadratic term: y = β 0 + β 1 x + β 2 x 2 + ε , where ε is the error and β 0 is the intercept, which we'll ignore here; we also omit the block terms for the sake of simplicity), the D-optimal design is 3–3–3 (at 0, 50 and 100 ng/ml, respectively) within each block.

In many settings, the goal is to learn about whether and how factors affect the response (i.e., whether β 1 and/or β 2 are non-zero and, if so, how far from zero they are), in which case the D-criterion is a good choice. In other cases, the goal is to find the level of the factors that optimizes the response, in which case a design that produces more precise predictions is better. The I-criterion, which minimizes the average prediction variance across the design region, is a natural choice.

In our example, the I-optimal design for the linear model is equivalent to that generated by the D-criterion: within each block, it allocates either four or five units to the low level and the rest to the high level. However, the I-optimal design for the model that includes both linear and quadratic effects is 2–5–2 within each block; that is, it places two experimental units at the low and high levels of the factor and places five in the center.

The quality of these designs in terms of their prediction variance can be compared using fraction of design space (FDS) plots 3 . We show this plot for the D- and I-optimal designs for the quadratic case (Fig. 2a ). A point on an FDS plot gives the proportion of the design space (the fraction of the 0–100 ng/ml interval, across the blocks) that has a prediction variance less than or equal to the value on the y axis. For instance, the I-optimal design yields a lower median prediction variance than the D-optimal design: at most 0.13 for 50% of the design space as compared to 0.15. Because of the extra runs at 50 ng/ml, the I-optimal design has a lower prediction variance in the middle of the region than the D-optimal design, but variance is higher near the edges (Fig. 2b ).

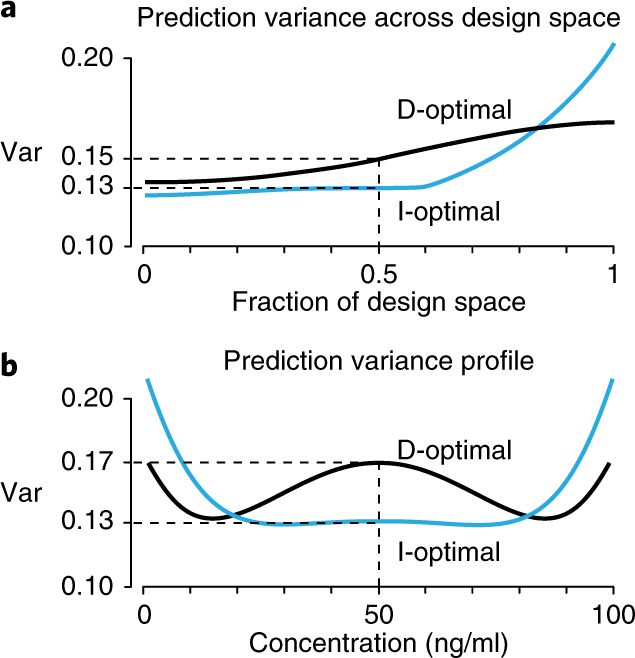
a , Prediction variance as a function of the fraction of design space (FDS). b , The variance profile across the range of concentrations for both designs.

Our one-factor blocking example demonstrates the basics of optimal design. A more realistic experiment might involve the same blocking structure but three factors—each with a specified range—and a goal to determine how the response is impacted by the factors and their interactions. We want to study the factors in combination; otherwise, any interactions between them will go undetected and the statistical efficiency to estimate factor effects is reduced.

Without the blocking constraint, a typical strategy would be to specify and use a high and low level for each factor and to perform an experiment using several replicates of the 2 3 = 8 treatment combinations. This is a classical two-level factorial design 4 that under reasonable assumptions provides ample power to detect factor effects and two-factor interactions. Unfortunately, this design doesn’t map to our scenario and can’t use the full nine-unit capacity of each shelf—unlike an optimal design, which can (Fig. 3 ).

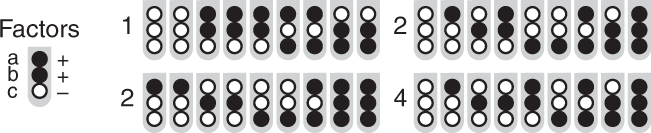
The D-optimal design that assigns three factors (a–c) at two levels each—low (unfilled circles) and high (filled circles)—to nine tubes on each of four shelves. The shelves are blocks and the design accounts for the main effects of the three factors and the three two-factor interactions. Each treatment is replicated at least four times, with treatments in tubes 3–7 on each shelf replicated five times.

In unconstrained settings where a classical design would be appropriate, optimal designs often turn out to be the same as their traditional counterparts. For instance, any RCBD 1 is both D- and I-optimal. Or, for a design with a sample size of 24, three factors, no blocks, and an assumed model that includes the three factor effects and all of the two-factor interactions, both the D- and I-criteria yield as optimal the two-level full-factorial design with three replicates.

So far, we have described optimal designs conceptually but have not discussed the details of how to construct them or how to analyze them 5 . Specialized software to construct optimal designs is widely available and accessible. To analyze the designs we’ve discussed—with continuous factors—it is necessary to use regression 2 (rather than ANOVA) to meaningfully relate the response to the factors. This approach allows the researcher to identify large main effects or quadratic terms and even two-factor interactions.

Optimal designs are not a panacea. There is no guarantee that (i) the experiment can achieve good power, (ii) the model form is valid and (iii) the criterion reflects the objectives of the experiment. Optimal design requires careful thought about the experiment. However, in an experiment with constraints, these assumptions can usually be specified reasonably.

Krzywinski, M. & Altman, N. Nat. Methods 11 , 699–700 (2014).

Article   PubMed   CAS   Google Scholar  

Krzywinski, M. & Altman, N. Nat. Methods 12 , 1103–1104 (2015).

Zahran, A., Anderson-Cook, C. M. & Myers, R. H. J. Qual. Tech. 35 , 377–386 (2003).

Article   Google Scholar  

Krzywinski, M. & Altman, N. Nat. Methods 11 , 1187–1188 (2014).

Goos, P. & Jones, B. Optimal Design of Experiments: A Case Study Approach (John Wiley & Sons, Chichester, UK, 2011).

Download references

Author information

Authors and affiliations.

Associate Professor of Statistics at Miami University, Oxford, OH, USA

Byran Smucker

Staff scientist at Canada’s Michael Smith Genome Sciences Centre, Vancouver, British Columbia, Canada

Martin Krzywinski

Professor of Statistics at The Pennsylvania State University, University Park, PA, USA

Naomi Altman

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Martin Krzywinski .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Smucker, B., Krzywinski, M. & Altman, N. Optimal experimental design. Nat Methods 15 , 559–560 (2018). https://doi.org/10.1038/s41592-018-0083-2

Download citation

Published : 31 July 2018

Issue Date : August 2018

DOI : https://doi.org/10.1038/s41592-018-0083-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Maximizing dataset variability in agricultural surveys with spatial sampling based on maxvol matrix approximation.

• Anna Petrovskaia
• Mikhail Gasanov
• Ivan Oseledets

Precision Agriculture (2025)

Development, optimization, and characterization of vitamin C-fortified oleogel-based chewable gels and a novel nondestructive analysis method for the vitamin C assay

• Reyhaneh Sabourian
• Farid Abedin Dorkoosh
• Mannan Hajimahmoodi

Food Production, Processing and Nutrition (2024)

Digital twins for electric propulsion technologies

• Maryam Reza
• Farbod Faraji
• Aaron Knoll

Journal of Electric Propulsion (2024)

Optimal experimental design for precise parameter estimation in competitive cross-reaction equilibria

• Somaye Vali Zade
• Hamid Abdollahi

Journal of the Iranian Chemical Society (2024)

Augmented region of interest for untargeted metabolomics mass spectrometry (AriumMS) of multi-platform-based CE-MS and LC-MS data

• Lukas Naumann
• Adrian Haun
• Christian Neusüß

Analytical and Bioanalytical Chemistry (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.